신입 게임 개발자의 프로그래밍 일기
[게임에서의 길찾기] 다익스트라(Dijkstra) 본문
[본 글은 개인 공부를 위해서 작성하는 글이며, 제공하는 정보에 오류가 있을 수 있습니다.
만약 오류를 발견하신 분은 댓글 작성을 부탁드립니다.]
게임에서의 길찾기 포스팅 글들은 게임에서 어떻게 길찾기들이 수행되는 지에 대해 공부하며 작성한 글입니다.
작성자의 능력이 미흡하여 구현된 코드의 수준도 미흡할 수 있는 점 양해부탁드립니다.
본 포스팅에서 사용할 미로는 다음과 같습니다.

6행 6열의 셀들로 구성되어 있는 격자형(Grid) 미로이며 다음과 같은 특징들을 갖습니다.
- 미로의 이동은 상, 하, 좌, 우로만 이동이 가능하며 대각선 이동은 불가능하다고 가정합니다.
- 미로의 셀 사이에서의 이동 비용은 모두 동일하다고 가정합니다.
다익스트라(Dijkstra) 알고리즘
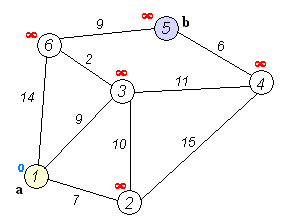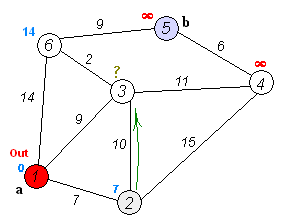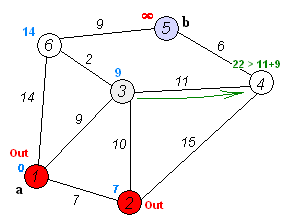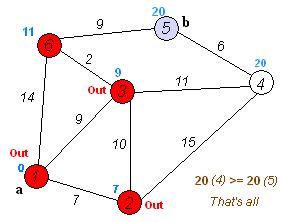
다익스트라 알고리즘은 이전 포스팅에서 다루었던 DFS와 BFS와 다르게
간선에 가중치가 있는 최단 경로 길찾기 알고리즘입니다.
그러므로 본격적인 길찾기 진행 전에, 먼저 격자형 미로를 그래프(Graph) 형태로 변형한 후에 진행하였습니다.
[격자형 미로 -> 그래프]
1. 격자형 미로를 그래프 자료구조 형태로 변화하기 위해 다음과 같은 기준들로 노드(Node)를 생성하였습니다.
1-1. 출발지 셀은 노드이다.
//void Maze2Graph(const vector<vector<MAZE_ELEMENT>>& maze, const int maze_size, vector<int>& nodeIdx2ElementIdx, vector<vector<int>>& graph, int& startNodeIdx, int& goalNodeIdx) 일부분(2020.12.11 기준)
if (MAZE_ELEMENT::START == maze[i][j])
{
nodeList.emplace_back(idx);
maze_node[i][j] = curNodeIdx;
startNodeIdx = curNodeIdx;
curNodeIdx += 1;
}
1-2. 도착지 셀은 노드이다.
//void Maze2Graph(const vector<vector<MAZE_ELEMENT>>& maze, const int maze_size, vector<int>& nodeIdx2ElementIdx, vector<vector<int>>& graph, int& startNodeIdx, int& goalNodeIdx) 일부분(2020.12.11 기준)
else if (MAZE_ELEMENT::GOAL == maze[i][j])
{
nodeList.emplace_back(idx);
maze_node[i][j] = curNodeIdx;
goalNodeIdx = curNodeIdx;
curNodeIdx += 1;
}
1-3. 인접한 셀 중 위, 아래 또는 좌, 우만이 동시에 이동 구역인 셀을 제외한 셀은 노드이다.
//void Maze2Graph(const vector<vector<MAZE_ELEMENT>>& maze, const int maze_size, vector<int>& nodeIdx2ElementIdx, vector<vector<int>>& graph, int& startNodeIdx, int& goalNodeIdx) 일부분 (2020.12.11 기준)
else
{
// 상, 우, 하, 좌
constexpr pair<int, int> direction[4] = { { 0, -1 },{ 1, 0 },{ 0, 1 },{ -1, 0 } };
int check[2] = { 0, 0 };
for (int k = 0; k < 4; ++k)
{
const int nextX = j + direction[k].first;
const int nextY = i + direction[k].secon
if (CanMove(maze, maze_size, nextX, nextY))
check[k % 2] += 1;
}
if ((2 == check[0] && 0 == check[1]) || (0 == check[0] && 2 == check[1]))
continu
nodeList.emplace_back(idx);
maze_node[i][j] = curNodeIdx;
curNodeIdx += 1;
}
위 기준으로 모든 셀들을 조사하여 나온 결과는 다음과 같습니다.

-1은 노드가 있는 셀을 의미하고, 그 이외의 숫자가 적힌 셀은 노드라는 것을 의미합니다.
추가로, 셀에 적힌 숫자는 노드로 변화하였을 때의 인덱스를 뜻합니다.
노드를 생성한 다음에는 간선(Edge)을 생성해야 합니다.
본 포스팅에서는 그래프를 인접행렬(Adjacency Matrix) 형태로 구현하였습니다.
2. 노드로 지정된 셀들을 시작점으로 탐색을 시작합니다.
노드마다 탐색은 상, 우, 하, 좌 순으로 총 4회 진행되며, 탐색시에는 오직 직진 방향으로만 이동합니다.
그리고 탐색은 이동 불가능 지역이나 노드로 지정된 다른 셀을 만날 때까지 수행합니다.
탐색이 종료되면서 마주친 셀이 노드일 경우, 간선을 생성합니다.
간선의 가중치는 탐색 중 거쳐온 셀의 개수와 동일합니다.
//void Maze2Graph(const vector<vector<MAZE_ELEMENT>>& maze, const int maze_size, vector<int>& nodeIdx2ElementIdx, vector<vector<int>>& graph, int& startNodeIdx, int& goalNodeIdx) 일부분 (2020.12.11 기준)
for (int elementIdx : nodeList)
{
nodeIdx2ElementIdx[curNodeIdx] = elementIdx;
const int originX = elementIdx % maze_size;
const int originY = elementIdx / maze_size;
// 상, 우, 하, 좌
constexpr pair<int, int> direction[4] = { { 0, -1 },{ 1, 0 },{ 0, 1 },{ -1, 0 } };
for (int i = 0; i < 4; ++i)
{
int curX = originX + direction[i].first;
int curY = originY + direction[i].second;
int weight = 1;
while (CanMove(maze, maze_size, curX, curY))
{
const int targetNodeIdx = maze_node[curY][curX];
if (-1 != targetNodeIdx)
{
graph[curNodeIdx][targetNodeIdx] = weight;
graph[targetNodeIdx][curNodeIdx] = weight;
break;
}
curX += direction[i].first;
curY += direction[i].second;
weight += 1;
}
}
++curNodeIdx;
}모든 노드들을 순회하면서 간선을 만들기 위한 탐색을 마치면 다음과 같은 그래프가 나타납니다.

[다익스트라 길찾기]
다익스트라를 우선순위 큐를 활용하여 구현하면 시간복잡도를 줄일 수 있지만
본 포스팅에서는 기본적인 형태의 다익스트라로 구현하였습니다.
1. 노드의 개수와 동일한 크기의 3종류의 vector 컨테이너를 생성합니다.
첫번째 vector는 비용 리스트로, 시작 노드에서 다른 노드로 이동할 때 필요한 최소 총 비용들이 기록됩니다.
초기값은 int형의 최대값입니다.
두번째 vector는 방문 리스트로, 노드마다 인접 노드들을 전부 방문했는지 여부를 체크하기 위해 사용합니다.
(임시로, 인접 노드를 전부 방문한 노드를 완전 방문이라고 말하겠습니다.)
세번째 vector는 부모 노드 리스트로, 길찾기가 완료된 후에 도착 노드를 시작으로 시작 노드까지 찾아가기 위해 사용합니다.
초기값은 -1로, -1은 길찾기 중 방문하지 않은 노드임을 뜻합니다.
//bool PathFinding_Dijkstra(const vector<vector<MAZE_ELEMENT>>& maze, Result& result) 일부분 (2020.12.11 기준)
vector<int> costList;
costList.resize(graph_size, INT_MAX);
vector<bool> visitList;
visitList.resize(graph_size);
vector<int> parentList;
parentList.resize(graph_size, -1);
2. 비용 리스트에 시작 노드까지의 비용 값으로 0을 기록합니다.
//bool PathFinding_Dijkstra(const vector<vector<MAZE_ELEMENT>>& maze, Result& result) 일부분 (2020.12.11 기준)
// 시작 지점
costList[startNodeIdx] = 0;3. 노드의 총 개수보다 1개 적은 횟수만큼 루프를 돌며 아래 처리들을 반복합니다.
3-1. 완전 방문하지 않은 노드들 중, 총 비용이 가장 적은 노드를 선택합니다.
//bool PathFinding_Dijkstra(const vector<vector<MAZE_ELEMENT>>& maze, Result& result) 일부분 (2020.12.11 기준)
int curMinimumCost = INT_MAX;
int curNodeIdx = -1;
for (int i = 0; i < graph_size; ++i)
{
if (visitList[i]) continue;
if (curMinimumCost > costList[i])
{
curMinimumCost = costList[i];
curNodeIdx = i;
}
}
3-2. 선택된 노드와 인접한 노드들을 조사하면서 인접 노드들의 비용 리스트를 갱신합니다.
그리고 만약 비용 리스트가 새로운 최소값으로 갱신되었다면 부모 노드 리스트에서 인접 노드의 부모 노드로
현재 선택된 노드의 인덱스를 기록합니다.
//bool PathFinding_Dijkstra(const vector<vector<MAZE_ELEMENT>>& maze, Result& result) 일부분 (2020.12.11 기준)
visitList[curNodeIdx] = true;
for (int adjNodeIdx = 0; adjNodeIdx < graph_size; ++adjNodeIdx)
{
const int weight = graph[curNodeIdx][adjNodeIdx];
// 간선이 없으면 스킵
if (0 == weight) continue;
const int newCost = costList[curNodeIdx] + weight;
if (costList[adjNodeIdx] > newCost)
{
costList[adjNodeIdx] = newCost;
parentList[adjNodeIdx] = curNodeIdx;
}
}
4. 부모 노드 리스트를 활용하여 최단 경로에 속한 노드들을 역순으로 구합니다.
//bool PathFinding_Dijkstra(const vector<vector<MAZE_ELEMENT>>& maze, Result& result) 일부분 (2020.12.11 기준)
list<int> pathList;
int searchNodeIdx = goalNodeIdx;
while (-1 != searchNodeIdx)
{
pathList.emplace_front(searchNodeIdx);
searchNodeIdx = parentList[searchNodeIdx];
}
최종적으로 다익스트라로 찾아낸 경로는 다음과 같습니다.

'GameProgramming' 카테고리의 다른 글
| [게임에서의 길찾기] DFS(Depth-First Search) (0) | 2020.12.01 |
|---|---|
| [게임에서의 길찾기] BFS(Breath-First Search) (0) | 2020.12.01 |
| [Direct3D9] Hardware Skinning 공부 중 - ID3DXMesh::CloneMeshFVF now fails for meshes with D3DFVF_XYZRHW (1) | 2020.08.05 |
| [Unreal Engine 4]이득우의 언리얼 C++ 게임 개발의 정석 - 코드 11_10 issue (0) | 2020.06.29 |


